Koll på matematik 2A

Koll på matematik 2B Lärarguide, Arbetsblad

P.g.a. ett trycktekniskt fel har arbetsbladen i Lärarguiden till Koll på matematik 2B, tryckning 4, fått facit ifyllt. Vi beklagar detta och erbjuder här de korrekta arbetsbladen för nedladdning.

Klicka här för att ladda ner Arbetsbladen till Koll på matematik 2B Lärarguide.pdf (PDF-dokument, 8,5 MB)

Facit

Facit till grundböckerna

Klicka här för att ladda ner facit till Koll på matematik 2A (PDF-dokument, 38,3 MB)

Klicka här för att ladda ner facit till Koll på matematik 2B (PDF-dokument, 35,5 MB)

Klicka här för att ladda ner facit till Koll på matematik 3A (PDF-dokument, 22,2 MB)

Klicka här för att ladda ner facit till Koll på matematik 3B (PDF-dokument, 20,4 MB)

Facit till arbetsblad i lärarguide

Klicka här för att ladda ner facit till arbetsbladen från Koll på matematik 1A lärarguide (PDF-dokument, 8,9 MB)

Klicka här för att ladda ner facit till arbetsbladen från Koll på matematik 1B lärarguide (PDF-dokument, 14,9 MB)

Klicka här för att ladda ner facit till arbetsbladen från Koll på matematik 2A Lärarguide (PDF-dokument, 6,4 MB)

Klicka här för att ladda ner facit till arbetsbladen från Koll på matematik 2B Lärarguide (PDF-dokument, 4,3 MB)

Klicka här för att ladda ner facit till arbetsbladen från Koll på matematik 3A Lärarguide (PDF-dokument, 7 MB)

Klicka här för att ladda ner facit till arbetsbladen från Koll på matematik 3B Lärarguide (PDF-dokument, 4,6 MB)

Facit till läxböcker

Klicka här för att ladda ner facit till Koll på matematik 1A läxbok (PDF-dokument, 5,3 MB)

Klicka här för att ladda ner facit till Koll på matematik 1B läxbok (PDF-dokument, 8,3 MB)

Klicka här för att ladda ner facit till Koll på matematik 2A läxbok (PDF-dokument, 4,3 MB)

Klicka här för att ladda ner facit till Koll på matematik 2B läxbok (PDF-dokument, 5,7 MB)

Klicka här för att ladda ner facit till Koll på matematik 3A läxbok (PDF-dokument, 5,3 MB)

Klicka här för att ladda ner facit till Koll på matematik 3B läxbok (PDF-dokument, 3,1 MB)

Här kan du läsa inlägg som författarna har gjort i sin Facebookgrupp -Koll på matematik 1-3

Syftet med färgerna
Färgerna är tydliga signaler för olika typer av innehåll! Allt för att både eleven och du som lärare snabbt ska kunna orientera dig i materialet och se syftet med olika typer av innehåll.

RÖTT - Start och introduktion till nytt kapitel. Möjlighet att kartlägga och öka elevernas förförståelse samt för dig att få ett nuläge för kommande undervisning.
GRÅTT - Grundsidor med kapitlets matematiska innehåll för gemensamt och enskilt arbete.
ROSA RUTA - Gemensamt resonemang och kommunikation kring ett matematiskt innehåll.
BLÅTT - De matematiska förmågorna synliggörs lite extra.
LILA - Återkoppling och bedömning.
GULT OCH GRÖNT - Självbedömning, samt ytterligare uppgifter som ger möjlighet till fler erfarenheter eller fördjupning utifrån visad förståelse.
MÖRKGULT - Begreppsförståelse (begreppsugglor)

Hoppas färgernas syfte har klarnat för dig!

#1 Språket – nyckeln till framgång!!!
Alla elever, svensktalande som nyanlända, gynnas av en språkutvecklande undervisning! I Koll på matematik bygger eleverna sitt matematiska språk redan från start. Varje kapitel inleds med gemensamt resonemang kring röda bildrutor.

Har du hört orden udda eller jämnt förut? I vilka sammanhang? Ge exempel!

Vad kan Alex mena när han säger att han har ett udda antal? Hur kan han veta det?

Vet du andra udda antal? Hur kan vi ta reda på om de är udda?

Elevernas tidigare erfarenheter synliggörs och deras förförståelse för det matematiska innehållet ökar. Läraren får viktig information om elevernas matematiska språk och ett utgångsläge inför sin kommande undervisning!

#2 ”Smaka” på ordet – vilka smaker känner du?
Alla elever, svensktalande som nyanlända, gynnas av en språkutvecklande undervisning! I Koll på matematik bygger eleverna sitt matematiska språk redan från start.

Vissa ”nya” ord och begrepp som eleverna möter i undervisningen finns redan i deras vardagsspråk. Men plötsligt får de en matematisk betydelse.

- ”Udda?!? Hm… det är väl när man är lite annorlunda, som när vi rockar udda sockor...”

Matematiskt används begreppet udda för att benämna tal som inte är delbara med två. Att förstå att vissa ord är homonymer, som skrivs eller uttalas lika men kan betyda olika saker, är inte självklart. Elever som lär på sitt andraspråk kan få stora problem med sådana ord MEN när de får uttrycka sig på både sitt första- och andraspråk samt får lyssna till och samtala med andra befinner de sig i en effektiv lärsituation.

Låt varje elev självbedöma sin förståelse inför ett nytt begrepp genom att markera ett av alternativen i Begreppsuggla 1. Med en Pratkompis får de sedan berätta om sina olika tankar för varandra. Lyft slutligen olika förståelser i ett gemensamt resonemang.

Att utgå ifrån varje elevs nuvarande föreställning och terminologi, och låta undervisningen haka i den, är effektivt då eleven ska utveckla ett matematiskt språk!

#3 En pratkompis – delar med sig av kompetens!
Alla elever, svensktalande som nyanlända, gynnas av en språkutvecklande undervisning! När elever för samtal om matematik och frågar varandra om saker och ting befinner de sig i ett kraftfält av lärande.

Med en PRATKOMPIS får eleven pröva olika tankar, reflektera, ställa frågor och kanske omvärdera sin nuvarande förståelse eller kunskap för till exempel ett nytt begrepp.

Efter elevens självbedömning, kring förståelse av t ex ett begrepp, kan PRATKOMPIS-PAR bildas utifrån aktuellt syfte och behov. Variera hur paren delas in. Då förs lärandet framåt för alla! Till exempel:

Röd med gul eller grön – Elever som markerat gult eller grönt blir resurser som med egna ord kan berätta om eller förklara ett begrepps innebörd för elever som markerat rött. Dessa kan i sin tur ställa frågor.
Gul med grön – Elever som markerat gult får berätta vad de vet för någon som är säker. Elever som markerat grönt får möjlighet att förklara.
Grön med grön – Elever som markerat grönt får utbyta sina olika erfarenheter kring begreppet med exempel hämtade ur deras egen verklighet, för att på så sätt vidga sitt kunnande.

#4 ”Kniven måste slipas samtidigt som den används!
”Alla elever, svensktalande som nyanlända, gynnas av en språkutvecklande undervisning! Nyanlända elevers vardagsspråk hör hemma i modersmålet. Under tiden som de lär sig svenska som andraspråk behöver deras förstaspråk få användas i lärandet.

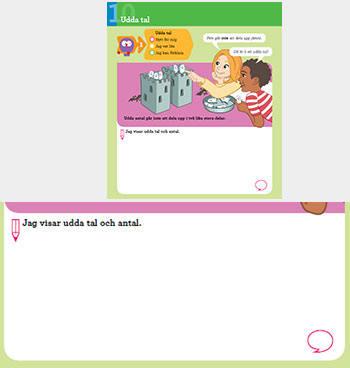
Nya begrepp behöver läras i situationer där sammanhang och ämnesinnehåll samverkar. Sammanhanget kan hämtas ur elevernas vardag, i det här fallet en lek med spökisar. Ämnesinnehållet är här begreppen udda tal och jämna tal. Samtala om bilden. Resonera med eleverna om hur spökisarna är uppdelade mellan tornen. Gör övningen ”praktiskt” med plockmaterial och låt eleverna pröva att använda begreppen i övningen.
Ställ till exempel frågor som:
Hur många torn är det? Hur många spökisar finns i tornen?
Hur vet du att det inte är lika många spökisar i varje torn?
Vad menar Ella när hon säger att ”Fem går inte att dela upp jämnt?”
Vad menar Alex när han säger att ”Då är 5 ett udda tal!”

Undersök andra antal. Hur vet vi om de är udda eller jämna? Klargör och kontrastera udda tals respektive jämna tals egenskaper. Skriv upp udda tal för sig, och jämna för sig. Leta efter talmönster etc.

#5 ”Ritrutan – ett flerspråkigt forum!
”Alla elever, svensktalande som nyanlända, gynnas av en språkutvecklande undervisning! Efter ett gemensamt resonemang kring ett nytt matematiskt begrepp eller innehåll (till exempel i en Rosa ruta, se #4) behöver varje elev få chans att visa sin nuvarande förståelse.

I Ritrutan kan eleverna använda flera uttrycksformer som bilder, ikoner, text och/eller symboler. Elever med annat modersmål bör här få uttrycka sig på sina förstaspråk eftersom det starkt gynnar deras kognitiva utveckling. Instruktioner till ritrutan kan i detta fall till exempel vara:
- Använd plockmaterial och pröva att dela upp olika antal praktiskt. Vilka antal går inte att dela upp jämnt i två delar, det vill säga, vilka är udda? Rita eller skriv.
- Använd idéer och tankar som du fick i det gemensamma resonemanget i den rosa rutan.
- Använd dina kunskaper om talmönster för att komma på olika udda tal!

När eleverna sedan får berätta om och visa sina Ritrutor för varandra, skapas ett gemensamt språk och referensramarna vidgas för det matematiska innehållet. Modersmålslärarens roll blir viktig för elever som behöver stöd i att ”översätta mellan olika språk” i sina Ritrutor. Förstaspråket utvecklas parallellt med ett svenskt skolrelaterat språk! När elevernas flerspråkighet bejakas och används som en resurs i klassrummet går lärandet framåt för ALLA elever!

#6 ”EPA – en kraftfull förkortning”
Alla elever, svensktalande som nyanlända, gynnas av en språkutvecklande undervisning! När eleverna har använt sig av olika uttrycksformer och språk för att visa sin förståelse i en Ritruta, behöver de få kommunicera den med varandra. Detta kan ske med hjälp av det språkutvecklande arbetssättet EPA.
E – Enskilt/eget, P – Par eller liten grupp, A – Alla.

I Koll på matematik är en röd pratbubbla i samband med olika uppgifter symbolen som uppmanar till EPA!

Kring begreppet udda i ritrutan kan det till exempel ske enligt följande:
E – Varje elev ritar av olika antal som är udda och/eller skriver tal som är udda.
P – Eleverna visar och berättar om sina udda antal och tal för varandra i par eller liten grupp. Uppmuntra dem gärna att komplettera sina Ritrutor med kompisarnas förslag.
A – Resonera tillsammans kring elevers olika exempel i helgrupp.

EPA leder till att ALLA elever blir delaktiga och bidrar med sina erfarenheter och kunskaper. EPA leder till att eleverna vidgar perspektiv, omvärderar och tillägnar sig ny kunskap. Och kanske viktigast av allt... EPA ger en upplevelse av att vara en viktig pusselbit i det gemensamma lärandet i klassrummet.

#7 ”HOO HOO!!! – Här kommer begreppsuggla”
Nu har eleverna självbedömt sin förståelse för ett nytt begrepp INFÖR arbetets start, lärt av och tillsammans med en Pratkompis och deltagit i gemensamma samtal och resonemang. Därefter har de även löst olika uppgifter på egen hand för att stärka sin förståelse. Nu är det dags att ta nästa steg, mitt under PÅGÅENDE arbete.

I Begreppskoll 2 möter de uggla 2 och får på nytt självbedöma sin nuvarande förståelse för aktuellt begrepp, här udda. (Här är inte röda ringen ”Nytt för mig” med, begreppet är troligtvis inte helt nytt för någon längre.) Upplevelsen av att kunna sätta ord på sin förståelse, på ett helt annat sätt nu jämfört med vid uggla 1, gör att eleven ser och konkret känner sitt lärande utvecklas.

Även här gynnas eleverna att få samtala med en Pratkompis för att få fler erfarenheter. Och inte minst för att få använda sitt förvärvade språk för att formulera vad de nu vet om udda!

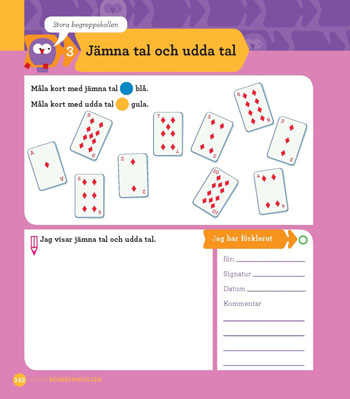
#8 ”Att äga begrepp ÄGER!”
När eleven visar förståelse för och kan förklara aktuellt begrepp kan eleven få visa det i Stora begreppskollen sist i elevboken. Eleven kan där rita, skriva och visa sin förståelse på olika sätt.
Tips till dig som lärare:
- Kommentera och ge feedback skriftligt.
- Datera och signera att du lyssnat till en förklaring som håller och är generaliserbar.
- Klipp ut och spara Stora begreppskollen som dokumentation.
- Låt eleven bygga en begreppssamling av de urklippta sidorna.
- Uppmana eleven att ta hjälp av sin begreppssamling då begreppet aktualiseras på nytt.
- Låt eleven göra en ny begreppskoll när förståelsen förändras eller fördjupas. Då kan eleven jämföra den nya mot den gamla och kanske beskriva skillnaden. Eleven ser sitt lärande utvecklas!

#9 ”Begreppsburken – en burk full av go(r)dsaker!”
När nya begrepp lanseras kan de klippas ut från begreppsbladet och läggas i en burk. Kanske ligger det redan andra begrepp där sedan tidigare! Arbeta sedan med burken som introduktion till en lektion eller då det blir en liten stund ”över”.

1. Låt någon elev slumpvis dra ett begrepp ur burken.
2. Använd EPA. Eleven tänker enskilt vad han eller hon vet om begreppet. Eleverna berättar sedan för varandra i par.
3. Välj slumpvis ut några par som berättar för alla.
4. Låt andra elever bidra med ytterligare kunskap, som inte paren lyft.
5. Sammanfatta vad gruppen nu vet om begreppet. Resonera kring nya frågeställningar som kan ha uppkommit.

Det strategiska arbetet med att kontinuerligt låta eleverna formulera sig kring olika begrepp och lyssna till varandras förklaringar och frågor, stärker verkligen deras begreppsförståelse!

#10 ”Rätt pusselbit på rätt plats”
Att utveckla goda strategier för huvudräkning är som att lägga ett pussel! Varje pusselbit, strategi, utgör en liten del av det hela pusslet, att välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter. Varje bit passar ihop med andra bitar, strategier som har samband med varandra. Allteftersom pusslet växer kan strategierna generaliseras och användas i utvidgade talområden.

Så småningom framträder ett tydligt motiv, en slags strategikarta att läsa av och använda vid olika beräkningar. Rätt strategi vid rätt tillfälle! För att kunna bli en skicklig huvudräknare behöver man utveckla god taluppfattning, kunskaper om talfakta och att se mönster och samband mellan tal och talområden. Dessutom krävs undervisning och en stor portion övning!

Några kommande inlägg handlar om några strategier, pusselbitar, som är utvecklingsbara, som håller att bygga vidare utifrån och som kan generaliseras.

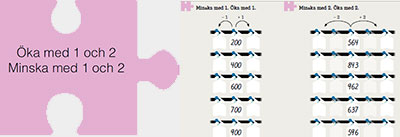
#11 ”Håll koll på dina grannar”
Genom att strukturerat möta effektiva huvudräkningsstrategier lär sig eleverna se samband mellan både tal och beräkningar. Det hjälper dem att automatisera återkommande beräkningar för att kunna avlasta sitt arbetsminne.

Följande strategier bygger på att eleverna uppfattar talen i en given talföljd:
Minska med 1 och Öka med 1 (talens grannar)
Minska med 2 och Öka med 2 (grannarnas grannar)
Här är tallinjen en mental framställning som eleven kan ta hjälp av för att utföra beräkningar. Till en början behöver tallinjen vara synlig för att på sikt kunna användas abstrakt.

Tallinje. En rät linje där varje punkt på linjen motsvarar ett reellt tal, till en början naturliga heltal. Talföljd. En följd av tal där differensen mellan två på varandra följande tal är densamma.

Vid beräkningar som kräver tiotalsövergång är denna kunskap viktig, framförallt i högre talområden. En elev som har en tydlig mental tallinje ser direkt att 301-299 = 2.

#12 ”Kärt barn har många namn”
Räknesättet subtraktion kan upplevas svårt av många elever. De kanske till och med har hört någon säga, "Vänta bara tills ni ska börja med minus..." Hur vi språkligt uttrycker oss kring subtraktion påverkar starkt elevernas möjlighet till förståelse.

Används begrepp som ta bort, minska, jämför, liten skillnad eller stor skillnad ostrukturerat/huller om buller eller som synonymer till varandra, för subtraktionsberäkningar, upplevs alldeles säkert räknesättet förvirrande för många elever.

I Koll på matematik tränar eleverna tidigt på att se på termerna i ett subtraktionsuttryck för att avgöra om det är effektivast att minska eller att jämföra talen och beräkna skillnaden. De lär sig bedöma om talen ligger nära varandra (liten skillnad) eller om talet som ska subtraheras, minuenden, är litet och kan minskas.

Vi vill inte att någon elev i första hand ska utföra beräkningen 301-299 i en uppställning. Elever som har en tydlig mental tallinje ser direkt att 301-299 ligger nära varandra, att talen därför bör jämföras och att skillnaden är liten.

#13 Pinus sylvestris & Pinus contorta
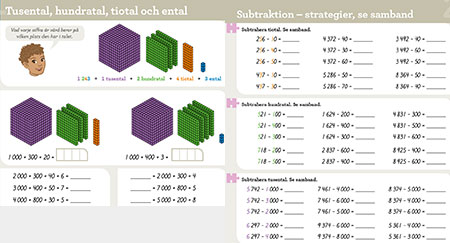
Att PINUS SYLVESTRIS och PINUS CONTORTA är Sveriges vanligaste tallsorter kanske eleverna inte behöver känna till, men att ental, tiotal, hundratal, tusental osv... är våra talsorter är desto viktigare och mer avgörande! Elevernas kunskaper om positionssystemet och tals uppbyggnad av olika talsorter är en viktig byggsten för att utveckla en god taluppfattning.Koll på matematik presenterar flera strategier där det till en början handlar om att till exempel subtrahera bara tiotal eller bara hundratal. Detta för att eleverna ska bli säkra på talsorterna och talens uppbyggnad. På sikt hjälper strategierna eleverna att utföra mer komplexa operationer där flera talsorter berörs.

#14 Tiokamrater – livslång vänskap
Tiokamrater är tal som tillsammans har summan 10, till exempel 1 + 9 och 2 + 8. Att vara helt säker på tiokamraterna är nödvändigt för att kunna generalisera olika beräkningar och se samband inom olika räknesätt och talområden. Eftersom vårt talsystem bygger på tiobas utgör tiokamraterna grunden för många strukturer och samband.
Tiokamraterna är till hjälp vid:
Addition
3 + 7 = 10, 30 + 70 = 100, 300 + 700 = 1000 osv.23 + 7 = 30, 230 + 70 = 300, 2300 + 700 = 3000 osv.
Subtraktion
10 - 3 = 7, 100 - 30 = 70, 1000 - 300 = 700 osv.50 - 3 = 47, 500 - 30 = 470, 5000 - 300 = 4700 osv.

#15 Problemlösning – en kreativ utmaning
Vi människor reagerar ofta på olika sätt då vi ställs inför en utmaning av något slag. Någon kikar lite nyfiket på den från håll, en annan ryggar förskräck tillbaka. En tredje känner sig grymt taggad och en fjärde avvaktar och tvekar. En fjärde ger upp utan att ens försöka medan en femte glatt kastar sig handlöst ut… Vilken inställning vi har beror nästan alltid på tidigare erfarenheter och av hur väl rustade vi är att möta utmaningen.

Många av våra elever kan känna på liknande sätt då de möter en uppgift i problemlösning, det vill säga en uppgift där de inte direkt ser lösningen, utan behöver undersöka och pröva sig fram. Vår uppgift som lärare är att rusta dem så de kan känna tillit till sin egen förmåga och mod att våga. Vi behöver dessutom ge dem relevanta verktyg och strategier att använda.

En tydlig och strukturerad undervisning i och kring problemlösning gör att elevernas utvecklar denna förmåga specifikt. I kommande serie med inlägg kommer vi presentera hur en sådan struktur kan se ut!

#16 En verktygslåda – med strategier
Visst… det GÅR att använda skaftet på en skruvmejsel för att spika in en mindre spik i väggen… men hammaren är mer effektiv. Vi bedömer först aktuell situation och väljer utifrån den ett lämpligt verktyg. I början viker sig lätt spiken, men efter viss träning går det att spika riktigt rakt med få slag av hammaren.

På samma sätt lämpar sig vissa problemlösningsstrategier bättre än andra för olika typer av problem. Eleverna behöver träna på och bli förtrogen med varje strategi för att kunna välja och använda den mest effektiva utifrån situation. Exempel på grundläggande lösningsstrategier kan vara att
- rita
- pröva
- sortera data och använda en tabell
- söka efter mönster och upprepningar

Dessa strategier presenteras i Koll på matematik 1–3. I läromedlet får eleverna träna på att använda dem olika typer av problem.

#17 ”Del 1 – Uppvärmningens betydelse – för att tagga match”
Få fotbollsspelare skulle tänka tanken att gå direkt ifrån omklädningsrummet till avsparken på planen. Lite löpträning, dribblande och passande med boll före matchen får igång kroppen och lagkänslan – tillsammans är vi starka! Genomgång av spelidé, peptalk och coaching av tränaren får igång det mentala tänket och ger ett gemensamt fokus – vi gör vårt bästa! På samma sätt kan det fungera vid problemlösning!

Eleverna värmer först upp gemensamt, tillsammans med läraren, genom ett enklare ”uppvärmningsproblem”, som till sitt matematiska innehåll liknar huvudproblemet. Därmed rustas eleverna för den väntande utmaningen och får bland annat
- förförståelse för det matematiska innehållet
- språklig stöttning kring aktuella matematiska begrepp
- utgå från sina egna tankar, tidigare erfarenheter och idéer
- träna en eller flera lämpliga lösningsstrategier
- lära av varandra och träna samarbete

I Koll på matematik 1–3 finns förslag på uppvärmningsproblem formulerade i Lärarguiden. De kan användas som förberedelse inför huvudproblemen i elevboken.

#18 ”Del 2 – Skarpt läge – matchstart"
Adrenalinpåslag… Nu gäller det att omsätta det man tränat på, djupledsbollar, passningsskugga… En god match bygger på att laget visar förståelse för varje spelare och att var och en bidrar och gör sitt bästa. En god laginsats handlar även om att göra sina lagkamrater bättre! Tränaren behöver vara förberedd på hur spelarna kan tänkas lösa situationer som kan uppstå i spelet. Tränaren stöttar och coachar under tiden och påvisar vad som är framgångsrikt och uppmuntrar sina spelare att våga ta egna beslut och att våga pröva egna idéer.

Elevbokens huvudproblem liknar uppvärmningsproblemet (se #17) i sitt matematiska innehåll. Genom att låta alla elever arbeta med samma problem, i par eller grupp, kan diskussionerna kring lösningarna bli givande. De kommunicerar och lär av varandra och varandras lösningsstrategier. Har läraren, precis som tränaren, förutsett de strategier eleverna troligast kommer att använda, kan denne enklare stötta, överblicka vilka strategier som används och ställa frågor som stödjer eller utmanar. Slutligen väljer läraren ut arbeten som lämpar sig för att presentera och diskutera gemensamt, som belyser lektionens matematiska idéer och som fördjupar lärandet.

I Koll på matematik 1–3 Lärarguide beskrivs hur läraren kan undervisa i problemlösning.

#19 ”Del 3 – Eftersnack och matchanalys”
- Vilket spel! Grymt bra samarbetat! Helt rätt inställning! Ta Stina och Sofia här som exempel…
- Inför nästa match ska vi träna mer på uppspel och fokusera på hur vi kan kommunicera mer med varandra på planen...
Efter matchen visar tränaren på styrkor och svagheter som framkommit i spelet. Tränaren visar även på vad nästa utvecklingssteg är för laget, men även för den enskilde spelaren.

På samma sätt kan läraren visa exempel på goda strategier eller sätt att visa sin lösning, samt låta eleverna reflektera över frågor som
- Vad lärde jag mig? Hur lärde jag mig? Vad kan jag lära mig av andras sätt att tänka? Hur kan jag göra nästa gång?
När läraren tar del av elevernas reflektioner får denne även en uppfattning om enskilda elevers styrkor respektive svagheter. Därigenom kan lärarens planering av den fortsatta undervisningen underlättas.

I Koll på matematik 1-3 Lärarguide beskrivs hur läraren kan undervisa i problemlösning